How Do You Know if an Object Is in Free Fall

Motion of a body subject field only to gravity

"Freeflight" redirects here. For the album past Ahmad Jamal, meet Freeflight (anthology).

In Newtonian physics, free autumn is whatsoever movement of a body where gravity is the merely forcefulness acting upon information technology. In the context of full general relativity, where gravitation is reduced to a infinite-fourth dimension curvature, a torso in complimentary fall has no force acting on it.

An object in the technical sense of the term "complimentary autumn" may not necessarily be falling down in the usual sense of the term. An object moving upwards might not usually be considered to be falling, simply if it is discipline to only the forcefulness of gravity, it is said to be in costless fall. The Moon is thus in free fall around the Globe, though its orbital speed keeps it in very far orbit from the World's surface.

In a roughly compatible gravitational field, in the absenteeism of any other forces, gravitation acts on each part of the trunk roughly equally. When at that place is no normal force exerted between a body (e.g. an astronaut in orbit) and its surrounding objects, it will result in the sensation of weightlessness, a status that also occurs when the gravitational field is weak (such as when far away from any source of gravity).

The term "free autumn" is often used more than loosely than in the strict sense divers above. Thus, falling through an atmosphere without a deployed parachute, or lifting device, is besides often referred to as free fall. The aerodynamic drag forces in such situations prevent them from producing full weightlessness, and thus a skydiver's "free autumn" after reaching terminal velocity produces the sensation of the body's weight existence supported on a cushion of air.

History [edit]

In the Western globe prior to the 16th century, it was more often than not assumed that the speed of a falling torso would be proportional to its weight—that is, a 10 kg object was expected to autumn x times faster than an otherwise identical 1 kg object through the same medium. The aboriginal Greek philosopher Aristotle (384–322 BC) discussed falling objects in Physics (Book VII), i of the oldest books on mechanics (run into Aristotelian physics). Although, in the 6th century, John Philoponus challenged this argument and said that, by ascertainment, ii balls of very different weights will fall at about the same speed.^[ane]

In 12th-century Iraq, Abu'fifty-Barakāt al-Baghdādī gave an explanation for the gravitational acceleration of falling bodies. According to Shlomo Pines, al-Baghdādī'due south theory of move was "the oldest negation of Aristotle'due south fundamental dynamic law [namely, that a constant strength produces a uniform motility], [and is thus an] anticipation in a vague fashion of the central law of classical mechanics [namely, that a force practical continuously produces acceleration]."^[two]

According to a tale that may be apocryphal, in 1589–92 Galileo dropped two objects of diff mass from the Leaning Tower of Pisa. Given the speed at which such a fall would occur, it is doubtful that Galileo could have extracted much information from this experiment. Most of his observations of falling bodies were actually of bodies rolling down ramps. This slowed things downward plenty to the point where he was able to mensurate the fourth dimension intervals with h2o clocks and his own pulse (stopwatches having non yet been invented). He repeated this "a full hundred times" until he had accomplished "an accuracy such that the departure between 2 observations never exceeded ane-tenth of a pulse beat." In 1589–92, Galileo wrote De Motu Antiquiora, an unpublished manuscript on the motion of falling bodies.^{[ citation needed ]}

Examples [edit]

Examples of objects in free fall include:

• A spacecraft (in space) with propulsion off (e.1000. in a continuous orbit, or on a suborbital trajectory (ballistics) going up for some minutes, and so downward).
• An object dropped at the height of a driblet tube.
• An object thrown upward or a person jumping off the ground at low speed (i.east. as long as air resistance is negligible in comparison to weight).

Technically, an object is in free fall even when moving upwards or instantaneously at rest at the tiptop of its move. If gravity is the only influence acting, so the acceleration is always downwardly and has the same magnitude for all bodies, usually denoted ${\displaystyle yard}$ .

Since all objects fall at the aforementioned charge per unit in the absenteeism of other forces, objects and people volition experience weightlessness in these situations.

Examples of objects not in costless-fall:

• Flying in an aircraft: at that place is also an boosted force of lift.
• Standing on the ground: the gravitational forcefulness is counteracted by the normal strength from the basis.
• Descending to the Earth using a parachute, which balances the force of gravity with an aerodynamic drag force (and with some parachutes, an additional lift force).

The instance of a falling skydiver who has not yet deployed a parachute is non considered free fall from a physics perspective, since they experience a drag forcefulness that equals their weight once they have accomplished terminal velocity (meet below).

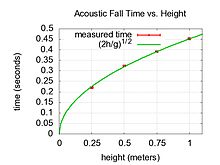
Measured fall time of a modest steel sphere falling from various heights. The information is in good understanding with the predicted fall fourth dimension of ${\displaystyle {\sqrt {2h/one thousand}}}$ , where h is the summit and g is the free-fall acceleration due to gravity.

About the surface of the Earth, an object in costless fall in a vacuum volition advance at approximately 9.eight 1000/s², independent of its mass. With air resistance acting on an object that has been dropped, the object will eventually reach a terminal velocity, which is around 53 yard/s (190 km/h or 118 mph^[3]) for a human skydiver. The last velocity depends on many factors including mass, drag coefficient, and relative surface area and volition simply be achieved if the fall is from sufficient altitude. A typical skydiver in a spread-eagle position will achieve terminal velocity after nigh 12 seconds, during which fourth dimension they volition have fallen around 450 m (ane,500 ft).^[3]

Free fall was demonstrated on the moon past astronaut David Scott on Baronial two, 1971. He simultaneously released a hammer and a plumage from the aforementioned height above the moon's surface. The hammer and the feather both fell at the same rate and hit the surface at the same time. This demonstrated Galileo's discovery that, in the absenteeism of air resistance, all objects experience the same acceleration due to gravity. On the Moon, all the same, the gravitational dispatch is approximately 1.63 m/southward^two, or just near ^one⁄₆ that on Globe.

Free fall in Newtonian mechanics [edit]

Compatible gravitational field without air resistance [edit]

This is the "textbook" case of the vertical motion of an object falling a small altitude shut to the surface of a planet. It is a skilful approximation in air as long as the force of gravity on the object is much greater than the force of air resistance, or equivalently the object'due south velocity is e'er much less than the final velocity (see below).

${\displaystyle v(t)=v_{0}-gt\,}$

${\displaystyle y(t)=v_{0}t+y_{0}-{\frac {1}{2}}gt^{ii}}$

where

${\displaystyle v_{0}\,}$ is the initial velocity (thou/s).

${\displaystyle v(t)\,}$ is the vertical velocity with respect to time (m/s).

${\displaystyle y_{0}\,}$ is the initial distance (1000).

${\displaystyle y(t)\,}$ is the distance with respect to time (m).

${\displaystyle t\,}$ is fourth dimension elapsed (s).

${\displaystyle g\,}$ is the acceleration due to gravity (nine.81 grand/southward² nigh the surface of the world).

If the initial velocity is zero, then the distance fallen from the initial position will grow as the foursquare of the elapsed time. Moreover, considering the odd numbers sum to the perfect squares, the distance fallen in successive fourth dimension intervals grows equally the odd numbers. This description of the behavior of falling bodies was given past Galileo.^[4]

Uniform gravitational field with air resistance [edit]

Dispatch of a small meteoroid when inbound the Earth's temper at different initial velocities

This case, which applies to skydivers, parachutists or whatever body of mass, ${\displaystyle m}$ , and cantankerous-sectional area, ${\displaystyle A}$ , with Reynolds number well above the critical Reynolds number, so that the air resistance is proportional to the foursquare of the fall velocity, ${\displaystyle v}$ , has an equation of motion

${\displaystyle m{\frac {\mathrm {d} v}{\mathrm {d} t}}=mg-{\frac {1}{2}}\rho C_{\mathrm {D} }Av^{2}\,,}$

where ${\displaystyle \rho }$ is the air density and ${\displaystyle C_{\mathrm {D} }}$ is the drag coefficient, assumed to be constant although in full general it volition depend on the Reynolds number.

Assuming an object falling from remainder and no change in air density with altitude, the solution is:

${\displaystyle v(t)=v_{\infty }\tanh \left({\frac {gt}{v_{\infty }}}\correct),}$

where the last speed is given by

${\displaystyle v_{\infty }={\sqrt {\frac {2mg}{\rho C_{D}A}}}\,.}$

The object'due south speed versus time tin can be integrated over time to find the vertical position as a function of time:

${\displaystyle y=y_{0}-{\frac {v_{\infty }^{ii}}{yard}}\ln \cosh \left({\frac {gt}{v_{\infty }}}\right).}$

Using the figure of 56 grand/s for the terminal velocity of a human, one finds that afterwards 10 seconds he will have fallen 348 metres and attained 94% of terminal velocity, and later on 12 seconds he volition have fallen 455 metres and will have attained 97% of terminal velocity. However, when the air density cannot exist assumed to be constant, such equally for objects falling from high altitude, the equation of motion becomes much more than difficult to solve analytically and a numerical simulation of the motion is unremarkably necessary. The figure shows the forces acting on meteoroids falling through the World's upper temper. HALO jumps, including Joe Kittinger's and Felix Baumgartner'southward record jumps, also belong in this category.^[5]

Inverse-square constabulary gravitational field [edit]

It can be said that two objects in space orbiting each other in the absence of other forces are in gratis autumn effectually each other, eastward.yard. that the Moon or an bogus satellite "falls around" the Earth, or a planet "falls around" the Sun. Bold spherical objects means that the equation of movement is governed by Newton's law of universal gravitation, with solutions to the gravitational two-body problem existence elliptic orbits obeying Kepler's laws of planetary motility. This connection betwixt falling objects close to the Earth and orbiting objects is best illustrated by the thought experiment, Newton's cannonball.

The motion of 2 objects moving radially towards each other with no angular momentum can be considered a special case of an elliptical orbit of eccentricity eastward = 1 (radial elliptic trajectory). This allows 1 to compute the free-autumn time for two indicate objects on a radial path. The solution of this equation of motion yields time every bit a function of separation:

${\displaystyle t(y)={\sqrt {\frac {{y_{0}}^{3}}{2\mu }}}\left({\sqrt {{\frac {y}{y_{0}}}\left(i-{\frac {y}{y_{0}}}\correct)}}+\arccos {\sqrt {\frac {y}{y_{0}}}}\right),}$

where

${\displaystyle t}$ is the time later on the start of the fall

${\displaystyle y}$ is the distance between the centers of the bodies

${\displaystyle y_{0}}$ is the initial value of ${\displaystyle y}$

${\displaystyle \mu =G(m_{1}+m_{two})}$ is the standard gravitational parameter.

Substituting ${\displaystyle y=0}$ we get the gratuitous-fall time.

The separation equally a function of time is given by the changed of the equation. The changed is represented exactly by the analytic power series:

${\displaystyle y(t)=\sum _{northward=i}^{\infty }\left[\lim _{r\to 0}\left({\frac {x^{north}}{n!}}{\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} r^{\,n-1}}}\left[r^{n}\left({\frac {seven}{2}}(\arcsin({\sqrt {r}})-{\sqrt {r-r^{two}}})\correct)^{-{\frac {two}{3}}north}\right]\right)\right].}$

Evaluating this yields:^{[6] [vii]}

${\displaystyle y(t)=y_{0}\left(10-{\frac {ane}{v}}x^{two}-{\frac {3}{175}}10^{3}-{\frac {23}{7875}}x^{4}-{\frac {1894}{3031875}}x^{five}-{\frac {3293}{21896875}}x^{half dozen}-{\frac {2418092}{62077640625}}x^{seven}-\cdots \correct)\ ,}$

where

${\displaystyle x=\left[{\frac {three}{2}}\left({\frac {\pi }{2}}-t{\sqrt {\frac {2\mu }{{y_{0}}^{3}}}}\right)\correct]^{2/3}.}$

Free fall in general relativity [edit]

In general relativity, an object in free fall is subject to no force and is an inertial body moving along a geodesic. Far away from whatever sources of infinite-time curvature, where spacetime is flat, the Newtonian theory of free autumn agrees with general relativity. Otherwise the ii disagree; e.thou., only full general relativity tin account for the precession of orbits, the orbital disuse or inspiral of meaty binaries due to gravitational waves, and the relativity of direction (geodetic precession and frame dragging).

The experimental observation that all objects in free fall accelerate at the same charge per unit, as noted by Galileo then embodied in Newton's theory as the equality of gravitational and inertial masses, and later confirmed to high accuracy by modern forms of the Eötvös experiment, is the basis of the equivalence principle, from which ground Einstein'due south theory of general relativity initially took off.

See besides [edit]

• Equations for a falling trunk
• One thousand-forcefulness
• Loftier-altitude military parachuting
• Micro-g surroundings
• Reduced-gravity aircraft
• Terminal velocity
• Weightlessness

References [edit]

1. ^ Morris R. Cohen and I. E. Drabkin (eds. 1958), A Source Book in Greek Science (p. 220), with several changes. Cambridge, MA: Harvard University Press, as referenced by David C. Lindberg (1992), The Beginnings of Western Science: The European Scientific Tradition in Philosophical, Religious, and Institutional Context, 600 B.C. to A.D. 1450, University of Chicago Press, p. 305, ISBN 0-226-48231-6
   • Note the influence of Philoponus' statement on Galileo'due south Ii New Sciences (1638)
2. ^ Pines, Shlomo (1970). "Abu'l-Barakāt al-Baghdādī , Hibat Allah". Lexicon of Scientific Biography. Vol. i. New York: Charles Scribner's Sons. pp. 26–28. ISBN0-684-10114-9.
   (cf. Abel B. Franco (October 2003). "Avempace, Projectile Move, and Impetus Theory", Journal of the History of Ideas 64 (iv), p. 521-546 [528].)
3. ^ ^{a b} "Complimentary autumn graph" (PDF). Green Harbor Publications. 2010. Retrieved 14 March 2016.
4. ^ Olenick, Richard P.; Apostol, Tom 1000.; Goodstein, David Fifty. (2008-01-fourteen). The Mechanical Universe: Introduction to Mechanics and Heat. Cambridge University Press. p. 18. ISBN978-0-521-71592-8.
5. ^ An analysis of such jumps is given in Mohazzabi, P.; Shea, J. (1996). "High distance free fall" (PDF). American Journal of Physics. 64 (10): 1242. Bibcode:1996AmJPh..64.1242M. doi:10.1119/1.18386.
6. ^ Foong, Southward Yard (2008). "From Moon-fall to motions under changed square laws". European Journal of Physics. 29 (five): 987–1003. Bibcode:2008EJPh...29..987F. doi:10.1088/0143-0807/29/5/012.
7. ^ Mungan, Carl East. (2009). "Radial Motility of Two Mutually Attracting Particles". The Physics Teacher. 47 (eight): 502–507. Bibcode:2009PhTea..47..502M. doi:10.1119/1.3246467.

External links [edit]

• Freefall formula calculator
• The Way Things Autumn an educational website

Wikimedia Commons has media related to Complimentary fall.

shafferdentrejecome.blogspot.com

Source: https://en.wikipedia.org/wiki/Free_fall

Share this post